EL RETO
Los gobiernos nacionales de la mayoría de los países alrededor del mundo descentralizan sus actividades administrativas entre entidades territoriales de menor nivel organizadas jerárquicamente; por ejemplo: departamentos-municipios, estados-condados, provincias-municipios, entre otros. Este tipo de divisiones subnacionales se conocen en la literatura con el nombre de “regiones normativas”. Las regiones normativas son la expresión de una voluntad política; sus límites se fijan de acuerdo con las tareas asignadas a las comunidades territoriales, a los tamaños de población necesarios para llevar a cabo estas tareas de manera eficiente y económica, o según factores históricos y/o culturales (Eurostat, 2006).

Sin embargo, existen dinámicas socioeconómicas que no necesariamente coinciden con la regiones normativas. Por ejemplo, los mercados laborales pueden involucrar múltiples municipalidades, lo cual suele delimitarse espacialmente en forma de regiones funcionales (Farmer and Fotheringham, 2011). Conjuntos de municipios pueden aglomerar industrias cuya interacción puede desencadenar procesos de innovación que deriven en mayor crecimiento económico (Duque, 2020). El crecimiento urbano puede desbordar las fronteras municipales creando conurbaciones que se convierten áreas metropolitanas (Squires, 2002). En cualquiera de los casos anteriores, una buena coordinación municipal es una condición sine qua non para la sana evolución de dichas dinámicas socioeconómicas.

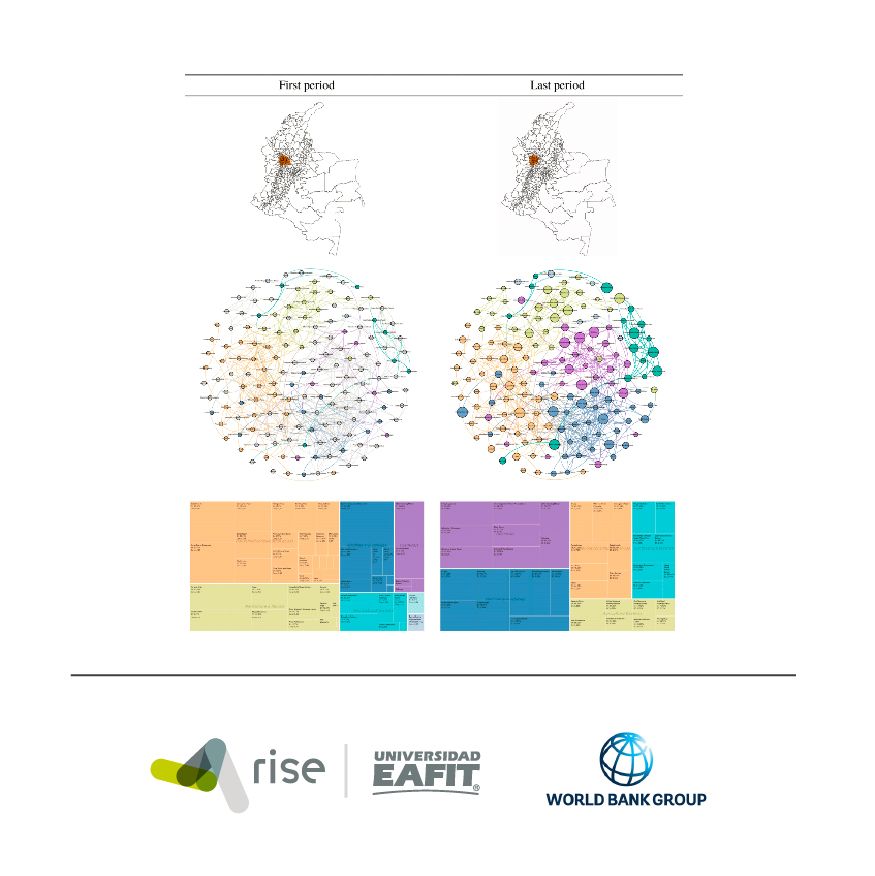
Pero, dado un fenómeno socioeconómico de interés, ¿cómo identificar la agrupación óptima de municipalidades que posibilite la implementación de políticas a la escala territorial adecuada?. La respuesta a esta pregunta forma parte de lo que se conoce en la literatura como diseño de regiones analíticas, y consiste en la agregación de unidades espaciales (por ejemplo municipios) en regiones espacialmente continuas (regiones) mientras se optimiza una función objetivo determinada (Duque et al., 2007). Las regiones analíticas posibilitan la implementación de políticas públicas más efectivas, una mejor focalización de recursos, una distribución más homogénea de los beneficios derivados de la política, y mayor cohesión entre los municipios que forman parte de una misma región (Fischer, 1980; Cörvers et al., 2009)

La solución al problema del diseño de unidades analíticas no es trivial. La agregación de n áreas en p regiones espacialmente continuas es un problema NP-duro, esto significa que la complejidad computacional aumenta exponencialmente al aumenta el número de áreas (Cliff y Haggett, 1970; Bixby, 2002). Debido a dicha complejidad la literatura ha formulado soluciones heurísticas que posibilitan encontrar buenas soluciones a instancias que serían imposibles de resolver por medio de los modelos exactos (Duque et al., 2007).

ÚLTIMOS DESARROLLOS
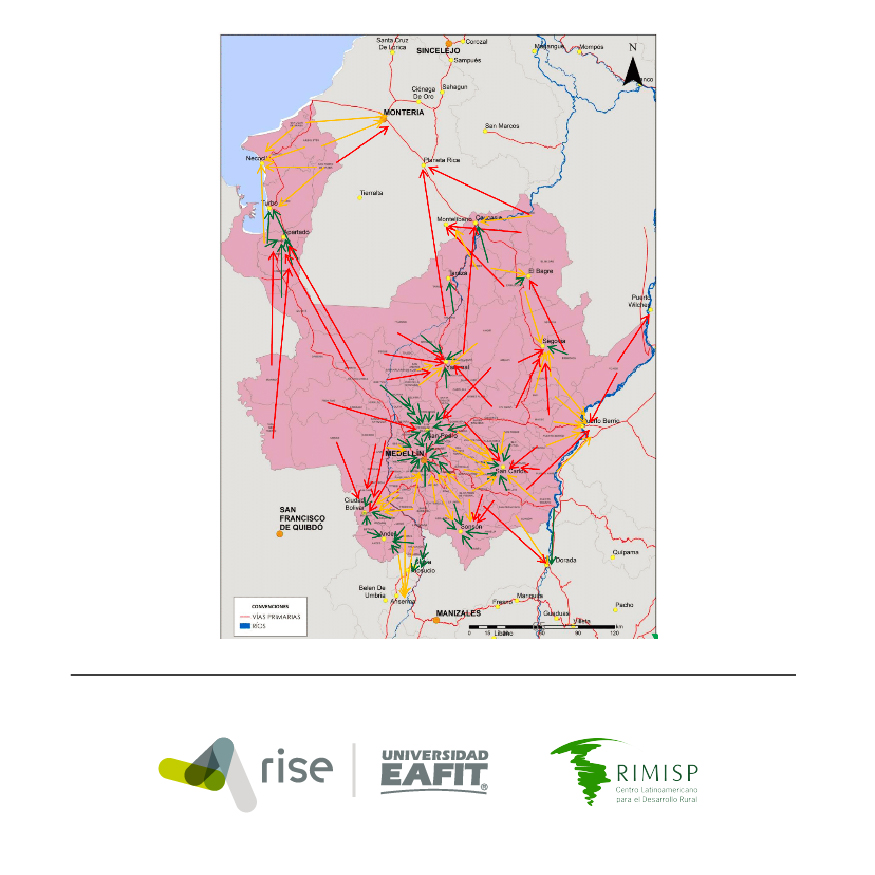
El grupo de investigación RiSE es uno de los líderes mundiales en el desarrollo de modelos para el diseño de regiones analíticas. Los algoritmos implementados por RiSE han sido publicados en revistas científicas de primer nivel (Duque et al., 2011; Duque et al., 2012; Duque et al., 2015; She et al., 2017; Church et al., 2020). Por medio de proyectos de transferencia RiSE a diseñado regiones analíticas para los gobiernos de Croacia (por medio del Banco Mundial)[1] y Colombia (por medio del Banco Mundial, Rimisp y el DNP)[2]. Los modelos implementados por RiSE, conocidos como la familia de los modelos p-regiones, han generado más de 511 citaciones en la literatura internacional.

Los heurísticos desarrollados por RiSE están implementados en ClusterPy[3], una librería multiplataforma escrita en lenguaje Python que proporciona una amplia gama de algoritmos para diseñar regiones analíticas (Duque et al., 2011b). Versiones básicas de los algoritmos de ClusterPy también han sido incorporados en programas como ArcGIS y QGIS (los dos software de Sistemas de Información Geográfica más populares en el mundo). ClusterPy (registro 13-62-133 del 2 de agosto de 2017. Direccion Nacional de Derecho de Autor. Unidad Administrativa Especial).

[1] The World Bank. Croatia Support for Establishment of a System for Strategic Planning and Management and for Preparation of the National Development Strategy 2030- RAS (P166454): Background Paper on functional-regions in Croatia.

[2] RIMISP- Latin American Center for Rural Development. Accompaniment to the Latin American Center for Rural Development (RIMISP) in the implementation of the subregionalization model of Colombia: Design a mathematical model for the subregionalization of Colombia. This project was developed within the framework of Contract No. 81219227 between RIMISP and the Deutsche Gesellschaft für Internationale Zusammenarbeit (GIZ) to support the National Planning Department (DNP), whose project has the objective of carrying out the functional subregionalization of Colombia.

[3] Registro 13-62-133 del 2 de agosto de 2017. Direccion Nacional de Derecho de Autor. Unidad Administrativa Especial.

Referencias:

Bixby, R. E. (2002). Solving real-world linear programs: A decade and more of progress. Operations Research 50: 3–15.

Church, R., Duque, J. C., & Restrepo, D. E. (2020). The p-Innovation ecosystems model. arXiv preprint arXiv:2008.05885.

Cliff, A. D., and P. Haggett (1970). On the efficiency of alternative aggregations in region-building problems. Environment and Planning 2: 285–94.

Cörvers, F., Hensen, M., and Bongaerts, D. (2009). Delimitation and coherence of

functional and administrative regions. Regional Studies, 43(1):19–31.

Duque, J. C., Anselin, L., & Rey, S. J. (2012). The max-p-regions problem. Journal of Regional Science, 52(3), 397-419.

Duque, J. C., Church, R. L., & Middleton, R. S. (2011). The p‐Regions Problem. Geographical Analysis, 43(1), 104-126.

Duque, J.C.; Dev, B.; Betancourt, A.; Franco, J.L. (2011b). ClusterPy: Library of spatially constrained clustering algorithms, Version 0.9.9. RiSE-group (Research in Spatial Economics). EAFIT University. https://www.rise-group.org.

Duque, J., Ramos, R., and nach., J. S. (2007). Supervised regionalization methods: A survey. International Regional Science Review, 30:195–220.

Duque, J. C., Ye, X., & Folch, D. C. (2015). spMorph: An exploratory space‐time analysis tool for describing processes of spatial redistribution. Papers in Regional Science, 94(3), 629-651.

Eurostat (2006). Nomenclature of territorial units for statistics—NUTS: Statistical regions of Europe.

Farmer, C. J., & Fotheringham, A. S. (2011). Network-based functional regions. Environment and Planning A, 43(11), 2723-2741.

Fischer, M. (1980). Regional taxonomy. A comparison of some hierarchic and non-

hierarchic strategies. Regional Science and Urban Economics, 10:503–537.

She, B., Duque, J. C., & Ye, X. (2017). The network-max-P-regions model. International Journal of Geographical Information Science, 31(5), 962-981.

Squires, G. D. (Ed.). (2002). Urban sprawl: Causes, consequences, & policy responses. The Urban Insitute.