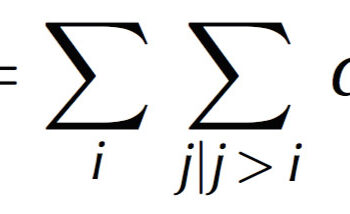http://onlinelibrary.wiley.com/doi/10.1111/j.1538-4632.2010.00810.x/abstract

The p-Regions Problem

Juan C. Duque (Universidad EAFIT)
Richard L. Church (University of California, Santa Barbara)
Richard S. Middleton (Los Alamos National Laboratory)

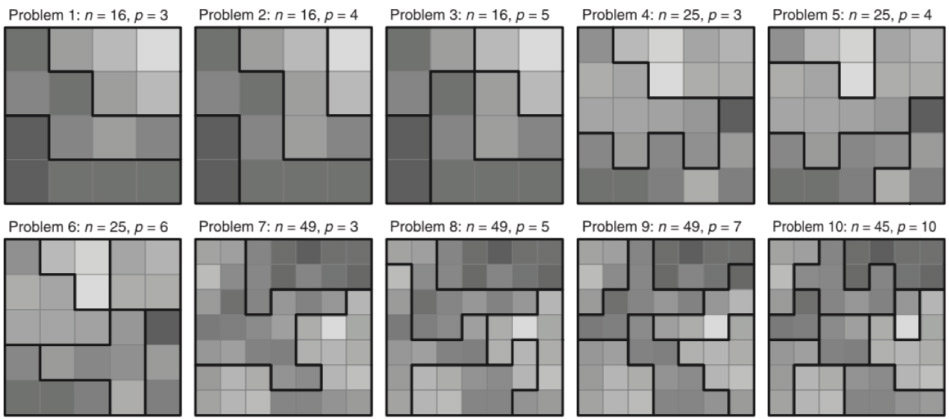
El problema de p-regiones se refiere a la agregación o agrupación de “n”áreas pequeñas en “p” regiones continuas, a la vez que se optimizan una o varias condiciones. El objetivo principal de este artículo es explorar posibles vías para la formulación de este problema en forma de programación lineal entera y mixta (MIP). La cuestión fundamental en la formulación de este problema es asegurar que cada región sea un conjunto de áreas pequeñas espacialmente continuo. Se presentan tres modelos de MIP para resolver el problema de p-regiones. Cada modelo minimiza la suma de diferencias entre todos los pares de las áreas dentro de cada región, sin dejar de garantizar su continuidad. Las tres estrategias diseñadas para asegurar la continuidad son: (1) una adaptación del modelo de Miller, Tucker, y Zemlin (1960) que hace uso de las restricciones desarrolladas para el problema del vendedor viajero (traveling salesman problem); (2) el uso de variables de asignación de área-ordenada (ordered-area assignment variables) basado en un ampliación del enfoque elaborado por Cova y Church (2000) para el problema de diseño de sitio geográfico (geographical site design problem); y, (3) el uso de restricciones de flujo basado en una extensión del trabajo por Shirabe (2005). Los autores ponen a prueba la eficacia de cada formulación y presentan una estrategia para reducir el tamaño del problema a ser solucionado.